5.卷积神经网络 - 一、卷积运算 - 《AI算法工程师手册》

1.1.1 卷积定义

可以利用观测结果的均值来估计飞船的位置。假设越近的观测结果越相关，于是对最近的观测结果赋予更高的权重。

令为权重函数，其中表示观测结果距离当前时刻的间隔，则得到时刻飞船真实位置的估计：

这种运算就称作卷积，用符号星号表示。

理论上可以为任意的实值函数，但是在这个示例中要求：
- 是个有效的概率密度函数，否则就不是一个加权平均。
- 在自变量为负数时，取值为零。否则涉及到未来函数，因为激光传感器只能输出时刻之前的观测结果。
通常当计算机处理数据时，连续的数据会被离散化，因此时间只能取离散值。

假设都是定义在整数时刻上，则得到离散形式的卷积：

实际操作中，因为只能存储有限的数据，所以这些函数的值在有限的点之外均为零。因此无限级数的求和最终是有限级数的求和。
在卷积神经网络中，函数称作输入，函数称作核函数，输出有时被称作特征图 feature map。
可以对多个维度进行卷积运算。

如果二维图像作为输入，则需要使用二维核函数，卷积运算的输出为：

其中表示二维图像的像素点的坐标，表示该坐标处的像素值。
- 通常的尺寸较大，如；而的尺寸较小，如
- 因为卷积是可交换的，所以可以等价写作：
  
  这称作翻转flip了核。
  
  卷积的可交换性在数学证明中有用，但是在神经网络中很少使用。

1.1.2 数学卷积与矩阵乘法

离散卷积可以视作输入矩阵与一个特殊的核矩阵的乘法。
- 对于一维的离散卷积，核矩阵的每一行必须和上一行移动一个元素后相等。
  
  这种类型的矩阵叫做Toeplitz矩阵。
- 对于二维的离散卷积，核矩阵对应着一个双重块循环矩阵。
  
  该矩阵大部分元素相等，且非常稀疏（几乎所有元素都为零）。
卷积运算可以转换成矩阵乘法，所以不需要对神经网络库的实现作出大的修改。

1.1.2.1 一维卷积和矩阵乘法

循环矩阵的定义：

可以利用循环矩阵求一维卷积。

1.1.2.2 二维卷积和矩阵乘法

二维卷积：

假设：
- 先将扩充到维：。扩充之后的新矩阵为。其中：
- 用构造一个列向量：将的第一行转置之后将其成为的前个元素；接下来是第二行的转置….第行的转置。
- 用这些循环矩阵构造一个大的块循环矩阵：
- 计算：。将的结果分配到的各行（与构造相反的过程），即得到二维卷积。

1.2 神经网络卷积

1.2.1 卷积定义

许多神经网络库会实现一个与卷积有关的函数，称作互相关函数cross-correlation。它类似于卷积：

有些机器学习库将它称作卷积。事实上在神经网络中，卷积指的就是这个函数（而不是数学意义上的卷积函数）。
神经网络的2维卷积的示例：

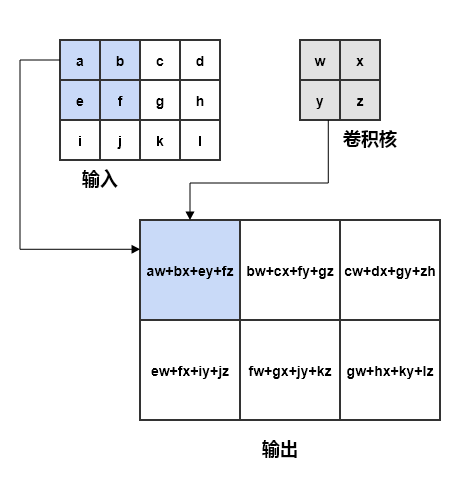
这里采用的是神经网络中卷积的定义：。其中，和由核函数决定。因为，所以他们的取值范围是。
单个卷积核只能提取一种类型的特征。

如果希望卷积层能够提取多个特征，则可以并行使用多个卷积核，每个卷积核提取一种特征。我们称输出的feature map 具有多个通道channel 。

feature map 特征图是卷积层的输出的别名，它由多个通道组成，每个通道代表通过卷积提取的某种特征。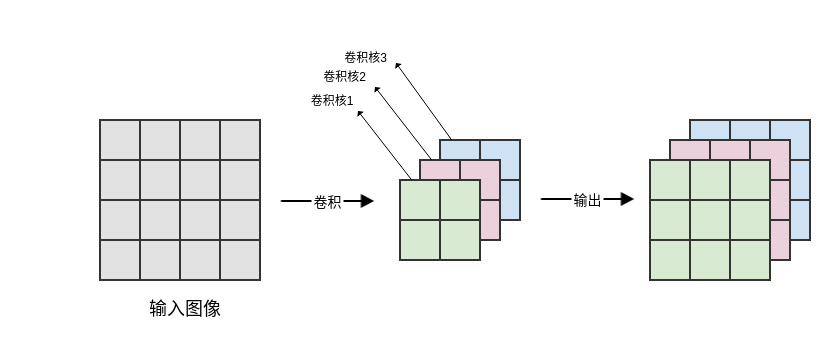
神经网络中，卷积运算的作用就类似于滤波，因此也称卷积核为filter 滤波器。
- 滤波器可以从原始的像素特征中抽取某些特征，如：边缘、角度、形状等。
  
  如：sobel 算子：
  
  其中表示检测垂直边缘的滤波器，它沿着水平方向做卷积；表示检测水平边缘的滤波器，它沿着垂直的方向做卷积。
  
  下图所示为一张原始的灰度图：
  
  经过卷积之后：
  
  经过卷积之后：
- 实际上，在卷积神经网络中我们并不会手工设计卷积核，而是通过学习算法自动学得卷积核中每个位置的值。

1.2.2 输入填充

在卷积神经网络中，可以隐式地对输入填充零，使其得到加宽。

如果未填充零，则网络每一层的宽度会逐层递减。根据卷积的性质，网络每一层宽度减少的数量等于卷积核的宽度减1。
- 如果卷积核尺寸较大，则网络的宽度迅速缩减，这限制了卷积神经网络的网络深度。
- 如果卷积核尺寸较小，则可用的卷积核的数量大幅度降低，这限制了卷积神经网络的表达能力。
对输入有三种填充零的方式：valid 填充、same 填充、full 填充。
valid 填充：不使用零来填充输入，卷积核只允许访问那些图像中能完全包含整个核的位置。

在valid 填充模式中，输出的大小在每一层都缩减。假设核的宽度是，则每经过一层，输出的宽度减少了。

如果输入图像的宽度是，则网络经过了层之后，输出的宽度变成。如果核的宽度非常大时，缩减非常明显。最终网络会缩减到 1 。
same 填充：使用足够的零来填充，使得输出和输入保持相同的大小。这是最常见的填充方式。
- 在填充模式中，网络可以包含任意多的卷积层，因为它不存在网络输出宽度缩减的问题。
- same 填充模式的一个问题是：输入的边缘单元可能存在一定程度上的欠表达。
  
  因为输入的中间区域的单元的影响域为全部的输出单元，这意味着这些输入单元的信息会被很多输出单元所编码。而输入的边缘区域的单元的影响域只是输出单元的一部分，这意味着这些输入单元的信息仅仅被少量输出单元所编码。
full 填充：在输入的两端各填充个零，使得每个输入单元都恰好被卷积核访问次。其中为卷积核的宽度。
- 假设核的宽度是，则每经过一层，输出的宽度增加了。
  
  如果输入图像的宽度是，则网络经过了层之后，输出的宽度变成。
- 它使得输入的边缘单元也能够得到充分表达。
- full 填充的一个问题是：输出的边界单元依赖于更少的输入单元。
  
  这使得学习到的结果在输出的中间部分表现较好，边缘部分的表现较差。

1.2.3 三维卷积

卷积神经网络的输入图片可以是二维（黑白图片），也可以是三维的（彩色图片）。

对于三维彩色图片，一个维度来表示不同的颜色通道（如红绿蓝），另外两个维度表示在每个通道上的空间坐标。
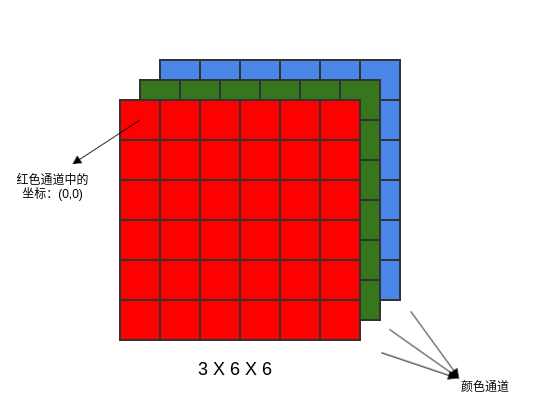
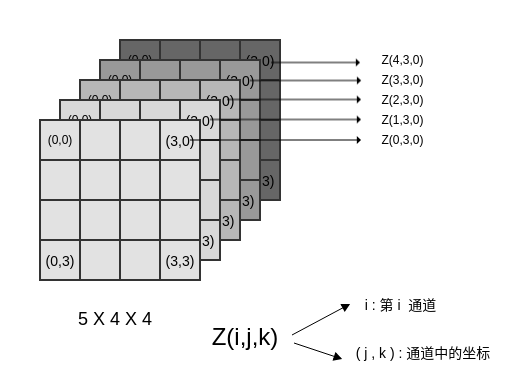
对于三维卷积：
- 假设输入为张量，每个元素是。其中：表示输入单元位于通道，表示通道中的坐标。
- 假设输出为张量，每个元素为。其中：表示输出单元位于通道，表示通道中的坐标。
  
  注意：输出的通道数量通常与输入的通道数量不等。
  
  输出有多个通道的原因是：使用了多个卷积核，每个卷积核会输出一个通道。
- 假设核张量为4维的张量，每个元素是。其中：表示输出单元位于通道，表示输入单元位于通道，表示通道中的坐标。
  
  则三维卷积可以表示为：
  
  其中：
  - 遍历了图像平面上的所有坐标。
  - 遍历了输入的所有通道。
  - 是单个三维卷积的核，多个并行的核的卷积结果组成了输出的多个通道。
上述表述中，张量、的通道索引位于坐标索引之前，这称作通道优先channel-first。

还有另一种模式：通道索引位于坐标索引之后，这称作channel-last 。

如：tensorflow 框架采用channel-last 的模式，theano 框架采用channel-first 的模式。这里默认采用的方式来描述。

1.2.4 降采样

如果对卷积层的输出进行降采样，则表示跳过图片中的一些位置。
- 优点：可以降低计算开销。因为它降低了卷积层的输出单元数量，也就降低了高层网络的输入单元数量。
- 缺点：提取的特征可能没有那么好，因为跳过的位置可能包含一些关键信息。
假设希望对输出的每个方向上，每隔个像素进行采样，则：

这里称作降采样卷积的步幅。
可以对不同的方向定义不同的步幅。

假设方向的步幅为，方向的步幅为，则有：
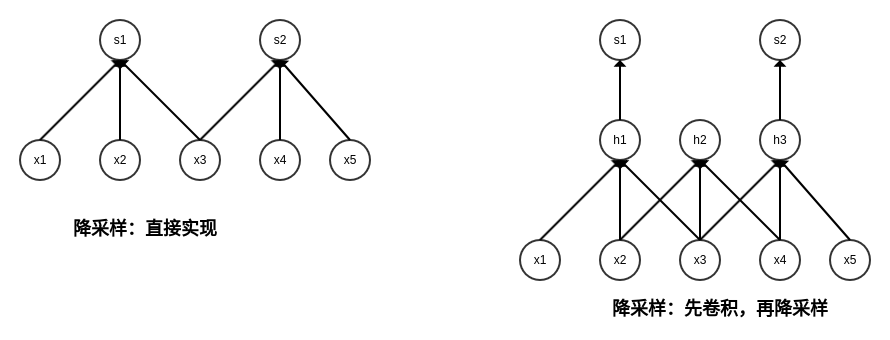
降采样卷积有两种实现形式：
- 通过直接实现步幅为 s 的卷积。
- 先进行完整的卷积，再降采样。这种做法会造成计算上的大量浪费，不建议采用。

1.2.5 梯度计算

实现卷积神经网络时，为了能够学习模型，必须能够计算核的梯度。

在某些简单情况下，核的梯度可以通过卷积来实现；大多数情况下（如：步幅大于1时），核的梯度无法通过卷积来实现。
卷积是一种线性运算，所以可以表示成矩阵乘法形式，涉及的矩阵是卷积核的函数。

该矩阵有两个特性：该矩阵是稀疏的；卷积核的每个元素都复制到该矩阵的很多个位置。
假设要训练一个卷积神经网络，它包含步幅为的步幅卷积，卷积核为，作用于多通道的图像。则卷积输出为：

假设需要最小化某个损失函数，则：
- 前向传播过程：计算，然后将传递到网络的其余部分来计算。
- 如果该层不是网络的输入层，则需要对求梯度来使得误差进一步反向传播。
  
  令，则有：
  
  根据的定义，有：
  
  则有：
  
  .