• 分类器 将输入 映射到它的真实类别 ，其中 是真实的映射函数。
• 深度前馈网络定义另一个映射 ，并且学习参数 从而使得 是 的最佳近似。

深度前馈网络之所以称作前馈的（），是因为信息从输入 到输出 是单向流动的，并没有从输出到模型本身的反馈连接。

如果存在反馈连接，则这样的模型称作循环神经网络（recurrent neural networks）。

深度前馈网络通常使用许多不同的函数复合而成，这些函数如何复合则由一个有向无环图来描述。最简单的情况：有向无环图是链式结构。

假设有三个函数 组成链式复合结构，则： 。其中： 被称作网络的第一层， 为网络第二层， 称为网络第三层。链的全长称作模型的深度。

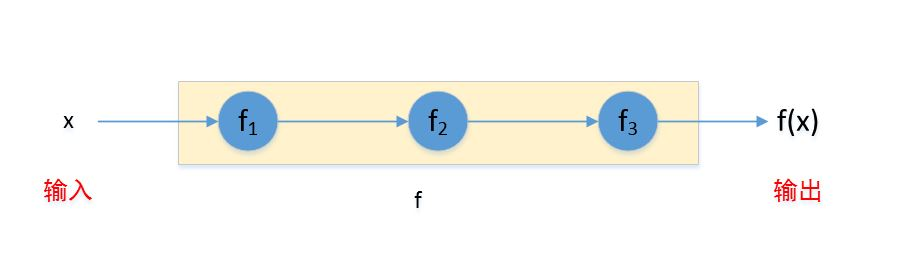
• 深度前馈网络的最后一层也称作输出层。输出层的输入为 ，输出为 。

• 给定训练样本 ，要求输出层的输出 ，但是对于其他层并没有任何要求。

  • 因为无法观测到除了输出层以外的那些层的输出，因此那些层被称作隐层(hidden layer) 。
  • 学习算法必须学习如何利用隐层来配合输出层来产生想要的结果。

也可以将每一层想象成由许多并行的单元组成，每个单元表示一个向量到标量的函数：每个单元的输入来自于前一层的许多单元，单元根据自己的激活函数来计算单元的输出。

因此每个单元类似于一个神经元。

线性模型简单高效，且易于求解。但是它有个明显的缺陷：模型的能力被局限在线性函数中，因此它无法理解任意两个输入变量间的非线性相互作用 。

解决线性模型缺陷的方法是：采用核技巧，将线性模型作用在 上，而不是原始输入 上。其中 是一个非线性变换。

可以认为：通过 ，提供了 的一个新的representation。

有三种策略来选择这样的非线性变换 。

• 使用一个通用的 ，如无限维的 （采用基于 RBF核的核技巧）。

  当 具有足够高的维数，则总是有足够的能力来适应训练集，但是对于测试集的泛化往往不佳。这是因为：通用的 通常只是基于局部平滑的原则，并没有利用足够多的先验知识来解决高级问题。

• 手动设计 。

  这种方法对于专门的任务往往需要数十年的努力（如语音识别任务）。

• 通过模型自动学习 。

  • 参数 ：从一族函数中学习 ，其中 定义了一个隐层。
  • 参数 ：将 映射到所需输出。

深度学习中，将参数化为 ，并使用优化算法来寻找 从而得到一个很好的 representation。

• 如果使用一个非常宽泛的函数族 ，则能获得第一种方案的好处：适应能力强。
• 如果将先验知识编码到函数族 中，则能获得第二种方案的好处：有人工先验知识。

因此深度学习的方案中，只需要寻找合适的、宽泛的函数族 ，而不是某一个映射函数 。

通过特征学习来改善模型不仅仅适用于前馈神经网络，也适用于几乎所有的深度学习模型。

训练一个深度前馈网络和训练一个线性模型的选项相同：选择优化算法、代价函数、输出单元的形式。

除此之外还需要给出下列条件：

• 深度前馈网络的网络结构也需要给出，其中包括：有多少层网络、每层网络有多少个单元、层级网络之间如何连接。

XOR函数是关于两个二进制值 的运算，其中 ，要求：

令想要学习的目标函数为：，其中 ，即 为输入 的两个分量。

假设模型给出了一个函数 ，希望学习参数 ，使得 尽可能接近 。

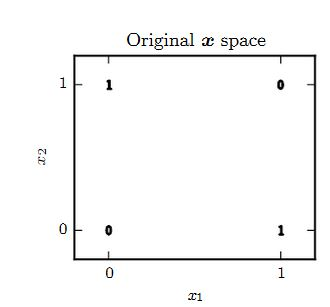
考虑一个简单的数据集 。希望 在这四个点上都尽可能接近 。

采用MSE损失函数： 。

假设选择一个线性模型： 。通过最小化 ，可以得到它的解为：

即： 。这意味着：线性模型将在每一点都是输出 0.5 ，因此它并不是函数的一个很好的拟合。

从下图可知：

• 当 时，函数的输出随着 的增加而增加。
• 当 时，函数的输出随着 的增加而减少。

因此导致了 ；同理 。

假设采用一个简单的深度前馈网络。该网络结构如下，它有一层隐层，并且隐层中包含两个单元。

• 第一层为隐层，对应于函数： ，其输入为 ，输出为 。
• 第二层为输出层，对应于函数： ，其输入为 ，输出为 。

大多数神经网络中， 的构造过程为：先使用仿射变换，然后通过一个激活函数。其中：激活函数不需要参数控制，仿射变换由参数控制。

令 ，其中 就是仿射变换， 为激活函数。

假设隐层的激活函数是线性的，则 也是线性的，暂时忽略截距项，则 。 即： 。

令： ，则有： 。即：前馈神经网络整体也是线性的。根据前面讨论，线性模型无法拟合xor 函数。因此 必须是非线性函数。

现代神经网络中，默认推荐的激活函数为修正线性单元(rectified linear unit:ReLU)： 。

整个网络为： 。

其中一个解为：

令 表示输入矩阵，每个样本占用一行。则对于输入空间中的全部四个点，输入矩阵为：

根据 ，有：

的每一行表示一个样本 对应的隐单元 。可以看到：隐层改变了样本之间的关系。

，得到：

.

在使用深度前馈网络逼近xor函数中，参数的求解可以通过简单的猜测来求解。但是对于复杂的函数逼近问题中，通常使用基于梯度的优化算法。

• 在实践中，梯度下降法通常难以找出像这样的容易理解的、整数值的解。