1. 正则化之后的目标函数为 ： 。

   • 为正则化项的系数，它衡量正则化项 和标准目标函数 的比重。

     • 则没有正则化。
     • 越大则正则化项越重要。
   • 如果最小化 ，则会同时降低 和参数 的规模。

2. 参数范数正则化可以缓解过拟合。

   如果 设置的足够大，则参数 就越接近零。这意味着模型变得更简单，简单的模型不容易过拟合（但是可能欠拟合）。

   对于神经网络，这意味着很多隐单元的权重接近0，于是这些隐单元在网络中不起任何作用。此时大的神经网络会变成一个小的网络。

   在 从 零逐渐增加的过程中存在一个中间值，使得参数 的大小合适，即一个合适的模型。

3. 选择不同的 的形式会产生不同的解，常见的形式有 正则化和 正则化。

1. 正则化通常被称作岭回归或者Tikhonov正则化。

   • 正则化项为 。系数 是为了使得导数的系数为 1。
   • 该正则化形式倾向于使得参数 更接近零。

2. 假设 参数就是权重 ，没有偏置参数，则： 。

   对应的梯度为： 。

   使用梯度下降法来更新权重，则权重的更新公式为： 。即：

   正则化对于梯度更新的影响是：每一步执行梯度更新之前，会对权重向量乘以一个常数因子来收缩权重向量。因此 正则化也被称作“权重衰减”。

1.1.1 整体影响

1. 令 ，它就是无正则化项时使得目标函数最小的权重向量。

   根据极小值的条件，有 。于是在 的邻域内泰勒展开 ：

   其中： 为 在 处的海森矩阵； 为 处的一个邻域。

   则 的梯度为： 。

2. 因为 是实对称矩阵，对其进行特征值分解：。 其中特征值组成对角矩阵 ，对应的特征向量组成正交矩阵 ：

   于是有：

   

   其中：

3. 正则化对模型整体的影响：沿着 的特征向量所定义的轴来缩放 。

   • 的第 个特征向量对应的 分量根据 因子缩放。
   • 沿着 特征值较大的方向受到正则化的影响较小。
   • 当 的方向对应的权重分量将被缩小到几乎为零。

1.1.2 物理意义

1. 在 点， 取得最小值；在 点（也就是图中的 点）， 和正则化项达到平衡（使得二者之和最小）。

   沿着 方向（横向）的 的曲率半径较大；曲率半径越大，曲率越小，特征值越小。

   • 曲率刻画曲线的弯曲程度。弯曲越厉害，则表示曲率半径越小、曲率越大。

     直线的曲率半径为 ，曲率为0。

   • 曲率半径是曲率的倒数。对于椭圆 ：

     • 在左右顶点：沿着 方向（纵向）的曲率半径为 。
     • 在上下顶点：沿着 方向（横向）的曲率半径为 。
     • 海森矩阵的特征值为： 。

2. 在上图中：

   • 的海森矩阵第一维 （ ）的特征值很小。

     所以当从 点水平移动时， 不会增加太多。因为 对这个方向没有强烈的偏好。所以正则化项对于该轴具有强烈的影响：正则化项将 拉向零。

   • 的海森矩阵第二维的特征值较大。

     对于 的变化非常敏感，因此正则化项对于该轴影响较小。

   • 因为沿着水平方向，一个较大的偏移只会对 产生一个较小的变化。因此正则化项倾向于从 点水平向零点移动。

3. 正则化表明：

   • 只有显著减小目标函数 的那个方向的参数会相对保留下来。
   • 无助于减小目标函数 的方向（该方向上 特征值较小，或者说该方向上 的曲率较小，或者说该方向上 的曲线更接近于直线），因为在这个方向上移动不会显著改变梯度，因此这个不重要方向上的分量会因为正则化的引入而被衰减掉。

1.1.3 示例

1. 考虑线性回归的 正则化，采用平方误差作为代价函数：

   

   这里忽略了线性回归的 的影响，这是为了便于说明解的性质。

2. 的解析解为： 。

   的解析解为： 。

   样本的协方差矩阵为 （这里已经将样本进行了标准化：减去了均值）， 为样本数量。因此 的对角线对应于每个输入特征的方差， 在对角线上增加了 。

   因此， 正则化使得：

   • 方差远大于 的特征受影响较小。
   • 只有方差接近甚至小于 的特征受影响较大。

1. 模型参数 的 的正则化形式为： 。即各个参数的绝对值之和。

2. 正则化后的目标函数 ： 。

   对应的梯度为 。其中 函数取自变量的符号：

   如果自变量大于零，则取值为 1；如果自变量小于零，则取值为 -1；如果自变量为零，则取值为零。

   使用梯度下降法来更新权重，给出权重的更新公式为：

   

   正则化对于梯度更新的影响是：不再是线性地缩放每个 （ 正则化项的效果），而是减去与 同号的常数因子。

1.2.1 整体效果

1. 令 ，它就是无正则化项时使得目标函数最小的权重向量。

   和 正则化中的推导相同，在 的邻域内泰勒展开：

   

1. 由于 正则化项在一般的海森矩阵情况下无法得到直接的代数表达式。

   因此我们进一步假设海森矩阵是对角矩阵。即：

   

   其中

   于是：

   

2. 考虑定义式，有：

   对于 来讲 ， 为常量。因此 的最小值由 决定。

   考虑每一个维度 ，可以考虑最优化目标：

   得到解析解： 。

3. 考虑 的情况。此时有两种可能：

   • ：则 。表示 正则化项将 推向 0 。
   • ：则 。此时 正则化项并不会将 推向 0，而是向零的方向推动了 的距离。

4. 考虑 的情况。此时有两种可能：

   • ：则 。表示 正则化项将 推向 0 。
   • ：则 。此时 正则化项并不会将 推向 0，而是向零的方向推动了 的距离。

   如果使用 正则化，则解为 。

1.2.2 物理意义

1. 如下所示：实线椭圆表示 的等值线，实线菱形表示正则化项 的等值线。

   在 点， 取得最小值；在 点（也就是图中的 点）， 和正则化项达到平衡（使得二者之和最小）。

   

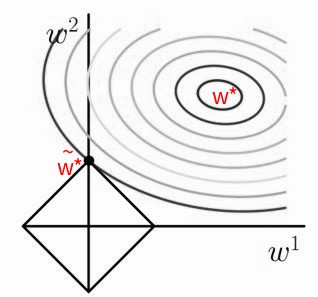
   可以看到 的等值线更容易与 正则化项的等值线在坐标轴相交从而取得整体极小值。

1. 正则化项更容易产生稀疏()解，而 正则化并不会导致稀疏解。

   • 在 正则化中， 的绝对值越小，该维的特征越容易被稀疏化。
   • 正则化的这一性质已经被广泛地用作特征选择： 正则化使得部分特征子集的权重为零，表明相应的特征可以被安全地忽略。

1. 许多正则化策略可以被解释为最大后验估计MAP：

   最大化后验估计等价于最小化代价函数。

   • 正则化项：参数的先验分布为高斯分布：

     忽略 项，因为它们与 无关。

   • 正则化项：参数的先验分布为各向同性拉普拉斯分布 ：

     忽略 项，因为它们与 无关。