• 当海森矩阵的条件数较大时，不同方向的梯度的变化差异很大。

  • 在某些方向上，梯度变化很快；在有些方向上，梯度变化很慢。

  • 梯度下降法未能利用海森矩阵，也就不知道应该优先搜索导数长期为负或者长期为正的方向。

    本质上应该沿着负梯度方向搜索。但是沿着该方向的一段区间内，如果导数一直为正或者一直为负，则可以直接跨过该区间。前提是：必须保证该区间内，该方向导数不会发生正负改变。

• 当海森矩阵的条件数较大时，也难以选择合适的步长。

  • 步长必须足够小，从而能够适应较强曲率的地方（对应着较大的二阶导数，即该区域比较陡峭）。
  • 但是如果步长太小，对于曲率较小的地方（对应着较小的二阶导数，即该区域比较平缓）则推进太慢。

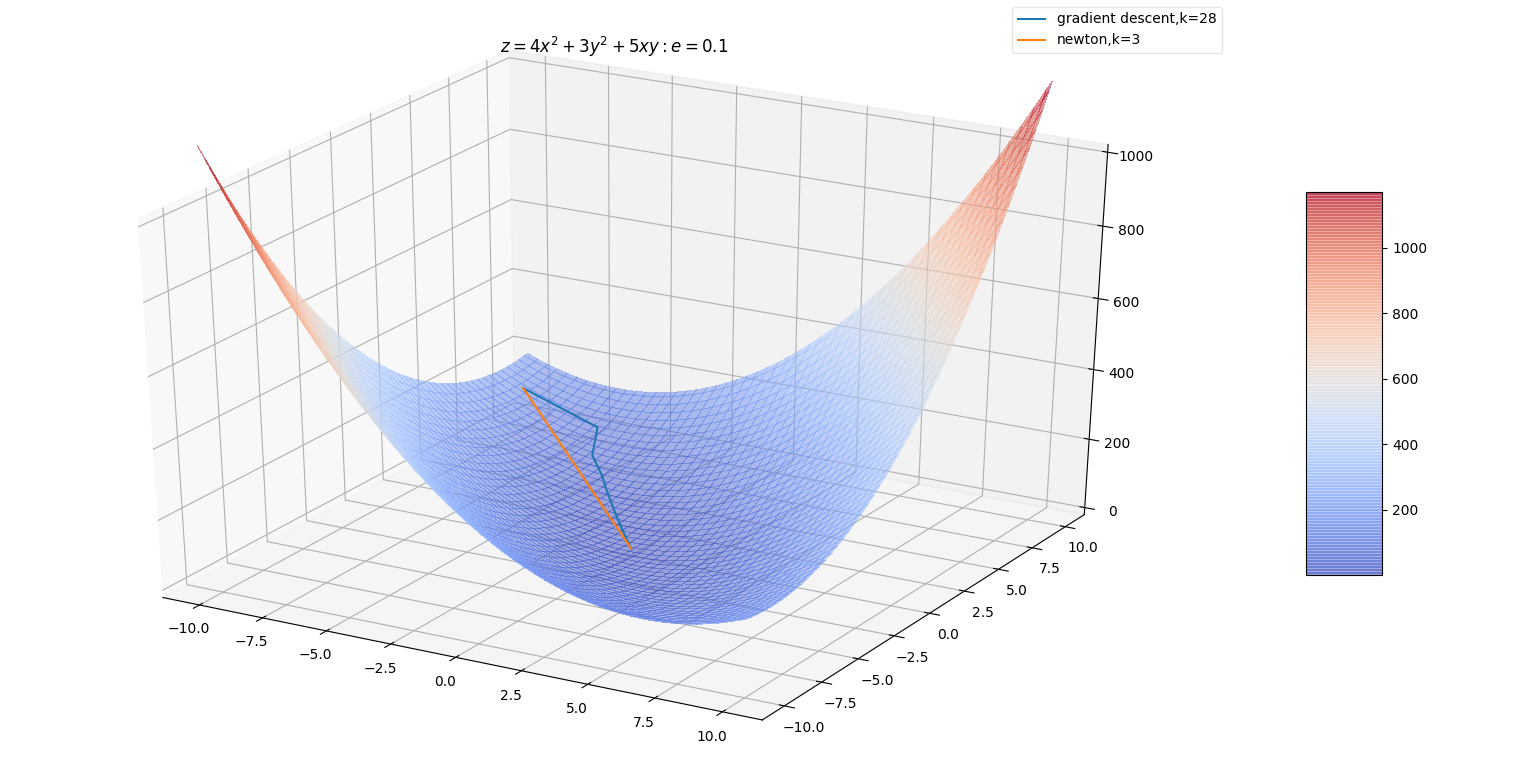
下图是利用梯度下降法寻找函数最小值的路径。该函数是二次函数，海森矩阵条件数为 5，表明最大曲率是最小曲率的5倍。红线为梯度下降的搜索路径。

牛顿法结合了海森矩阵。

考虑泰勒展开式： 。其中 为 处的梯度； 为 处的海森矩阵。

如果 为极值点，则有： ，则有： 。

• 当 是个正定的二次型，则牛顿法直接一次就能到达最小值点。
• 当 不是正定的二次型，则可以在局部近似为正定的二次型，那么则采用多次牛顿法即可到达最小值点。

当位于一个极小值点附近时，牛顿法比梯度下降法能更快地到达极小值点。

如果在一个鞍点附近，牛顿法效果很差，因为牛顿法会主动跳入鞍点。而梯度下降法此时效果较好（除非负梯度的方向刚好指向了鞍点）。

仅仅利用了梯度的优化算法（如梯度下降法）称作一阶优化算法，同时利用了海森矩阵的优化算法（如牛顿法）称作二阶优化算法。

牛顿法算法：

• 输入：

  • 目标函数
  • 梯度
  • 海森矩阵
  • 精度要求

• 输出： 的极小值点

梯度下降法中，每一次 增加的方向一定是梯度相反的方向 。增加的幅度由 决定，若跨度过大容易引发震荡。

而牛顿法中，每一次 增加的方向是梯度增速最大的反方向 （它通常情况下与梯度不共线）。增加的幅度已经包含在 中（也可以乘以学习率作为幅度的系数）。

深度学习中的目标函数非常复杂，无法保证可以通过上述优化算法进行优化。因此有时会限定目标函数具有连续，或者其导数连续。

• 连续的定义：对于函数 ，存在一个常数 ，使得：

凸优化在某些特殊的领域取得了巨大的成功。但是在深度学习中，大多数优化问题都难以用凸优化来描述。