• 发生可能性较大的事件包含较少的信息。
• 发生可能性较小的事件包含较多的信息。
• 独立事件包含额外的信息 。

对于事件 ，定义自信息为： 。

自信息仅仅处理单个输出，但是如果计算自信息的期望，它就是熵：

记作 。

• 熵刻画了按照真实分布 来识别一个样本所需要的编码长度的期望（即平均编码长度）。

  如：含有4个字母 (A,B,C,D) 的样本集中，真实分布 ，则只需要1位编码即可识别样本。

• 对于离散型随机变量 ，假设其取值集合大小为 ，则可以证明： 。

根据定义可以证明： 。

即：描述 和 所需要的信息是：描述 所需要的信息加上给定 条件下描述 所需的额外信息。

KL散度（也称作相对熵）：对于给定的随机变量 ，它的两个概率分布函数 和 的区别可以用 散度来度量：

• KL散度非负：当它为 0 时，当且仅当 P和是同一个分布（对于离散型随机变量），或者两个分布几乎处处相等（对于连续型随机变量）。

• KL散度不对称： 。

  直观上看对于 ，当 较大的地方， 也应该较大，这样才能使得 较小。

交叉熵：。

• 刻画了错误分布 编码真实分布 带来的平均编码长度的增量。

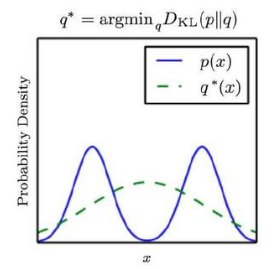
示例：假设真实分布 为混合高斯分布，它由两个高斯分布的分量组成。如果希望用普通的高斯分布 来近似 ，则有两种方案：

• 如果选择 ，则：

  • 当 较大的时候 也必须较大 。如果 较大时 较小，则 较大。
  • 当 较小的时候 可以较大，也可以较小。

  因此 会贴近 的峰值。由于 的峰值有两个，因此 无法偏向任意一个峰值，最终结果就是 的峰值在 的两个峰值之间。

  

• 如果选择 ，则：

  • 当 较小的时候， 必须较小。如果 较小的时 较大，则 较大。

  因此 会贴近 的谷值。最终结果就是 会贴合 峰值的任何一个。