Distributed Iterative Graph Processing (Pregel)
Check out the hands-onto learn more.
The processing system inside ArangoDB is based on:Pregel: A System for Large-Scale Graph Processing – Malewicz et al. (Google), 2010.This concept enables us to perform distributed graph processing, without the need for distributed global locking.
If you are running a single ArangoDB instance in single-server mode, there are no requirements regarding the modeling of your data. All you need is at least one vertex collection and one edge collection. Note that the performance may bebetter, if the number of your shards / collections matches the number of CPU cores.
When you use ArangoDB Community Edition in cluster mode, you might need to model your collections in a certain way toensure correct results. For more information see the next section.
To enable iterative graph processing for your data, you will need to ensurethat your vertex and edge collections are sharded in a specific way.
The Pregel computing model requires all edges to be present on the DB-Server wherethe vertex document identified by the value is located.This means the vertex collections need to be sharded by ‘_key’ and the edge collectionwill need to be sharded after an attribute which always contains the ‘_key’ of the vertex.
Our implementation currently requires every edge collection to be sharded after a “vertex” attributes,additionally you will need to specify the key distributeShardsLike and an equal number of shards on every collection.Only if these requirements are met can ArangoDB place the edges and vertices correctly.
For example you might create your collections like this:
You will need to ensure that all edges contain the proper values in their shard key attribute.For a vertex document with the following content { _key: "A", value: 0 }the corresponding edge documents would have to look as follows:
{ "_from":"vertices/A", "_to": "vertices/B", "vertex": "A" }{ "_from":"vertices/A", "_to": "vertices/C", "vertex": "A" }{ "_from":"vertices/A", "_to": "vertices/D", "vertex": "A" }...
As can be seen, all edges are using a value of A (the _key value of the vertex) in their shard key attribute “vertex”.
This will ensure that outgoing edge documents will be placed on the same DB-Server as the vertex.Without the correct placement of the edges, the Pregel graph processing system will not work correctly, becauseedges will not load correctly.
Arangosh API
Starting an Algorithm Execution
The Pregel API is accessible through the @arangodb/pregel package.To start an execution you need to specify the algorithm name and the vertex and edge collections.Alternatively you can specify a named graph. Additionally you can specify custom parameters whichvary for each algorithm.The start method will always a unique ID which can be used to interact with the algorithm and later on.
The below version of the start method can be used for named graphs:
var pregel = require("@arangodb/pregel");var execution = pregel.start("<algorithm>", "<yourgraph>", params);
params needs to be an object, the valid keys are mentioned below in the section
Alternatively you might want to specify the vertex and edge collections directly. The call-syntax of the startmethod changes in this case. The second argument must be an object with the keys vertexCollectionsand edgeCollections.
var pregel = require("@arangodb/pregel");var params = {};var execution = pregel.start("<algorithm>", {vertexCollections:["vertices"], edgeCollections:["edges"]}, {});
The last argument is still the parameter object. See below for a list of algorithms and parameters.
Status of an Algorithm Execution
The code returned by the pregel.start(…) method can be used totrack the status of your algorithm.
var execution = pregel.start("sssp", "demograph", {source: "vertices/V"});var status = pregel.status(execution);
Valid values for the state field include:
- “running” algorithm is still running
- “done”: The execution is done, the result might not be written back into the collection yet.
- “canceled”: The execution was permanently canceled, either by the user or by an error.
- “in error”: The execution is in an error state. This can be caused by primary DB-Servers being not reachable or being non responsive.The execution might recover later, or switch to “canceled” if it was not able to recover successfully
- “recovering”: The execution is actively recovering, will switch back to “running” if the recovery was successful
The object returned by the status method might for example look something like this:
{"state" : "running","gss" : 12,"totalRuntime" : 123.23,"aggregators" : {"max" : true,"phase" : 2},"sendCount" : 3240364978,"receivedCount" : 3240364975}
To cancel an execution which is still running, and discard any intermediate results you can use the cancel method.This will immediately free all memory taken up by the execution, and will make you lose all intermediary data.
You might get inconsistent results if you cancel an execution while it is already in its done state. The data is writtenmulti-threaded into all collection shards at once, this means there are multiple transactions simultaneously. A transaction mightalready be committed when you cancel the execution job, therefore you might see the result in your collection. This does not applyif you configured the execution to not write data into the collection.
ArangoDB supports retrieving temporary Pregel results through the ArangoDB query language (AQL). When our graph processing subsystem finishes executing an algorithm, the result can either be written back into the database or kept in memory. In both cases the result can be queried via AQL. If the data was not written to the databasestore it is only held temporarily, until the user calls the cancel method. For example, a user might want to queryonly nodes with the highest rank from the result set of a PageRank execution.
FOR v IN PREGEL_RESULT(<handle>)FILTER v.value >= 0.01RETURN v._key
By default, the PREGEL_RESULT AQL function will return the _key of each vertex plus the resultof the computation. In case the computation was done for vertices from different vertex collection,just the _key values may not be sufficient to tell vertices from different collections apart. In this case, the PREGEL_RESULT can be given a second parameter withId, which will make it returnthe _id values of the vertices as well:
FILTER v.value >= 0.01RETURN v._id
Please note that PREGEL_RESULT will only work for results of Pregel jobs that were stored withthe store parameter set to false in their job configuration.
Algorithm Parameters
There are a number of general parameters which apply to almost all algorithms:
store: Defaults to true. If true, the Pregel engine will write results back to the database.If the value is false then you can query the results via AQL.See AQL integration.maxGSS: Maximum number of global iterations for this algorithmparallelism: Number of parallel threads to use per worker. Does not influence the number of threads used to loador store data from the database (this depends on the number of shards).async: Algorithms which support async mode, will run without synchronized global iterations,might lead to performance increases if you have load imbalances.resultField: Most algorithms will write the result into this fielduseMemoryMaps: Use disk based files to store temporary results. This might make the computation disk-bound, butallows you to run computations which would not fit into main memory. It is recommended to set this flag forlarger datasets.shardKeyAttribute: shard-key that edge-collections are sharded after (default: )
Page Rank
PageRank is a well known algorithm to rank documents in a graph. The algorithm will run untilthe execution converges. Specify a custom threshold with the parameter threshold, to run for a fixednumber of iterations use the maxGSS parameter.
var pregel = require("@arangodb/pregel");pregel.start("pagerank", "graphname", {maxGSS: 100, threshold:0.00000001, resultField:'rank'})
Seeded PageRank
It is possible to specify an initial distribution for the vertex-documents in your graph. To define theseseed ranks / centralities you can specify a sourceField in the properties for this algorithm.If the specified field is set on a document and the value is numeric, then it will beused instead of the default initial rank of 1 / numVertices.
var pregel = require("@arangodb/pregel");pregel.start("pagerank", "graphname", {maxGSS: 20, threshold:0.00000001, sourceField:'seed', resultField:'rank'})
Single-Source Shortest Path
Calculates the distance of each vertex to a certain shortest path. The algorithm will run until it converges,the iterations are bound by the diameter (the longest shortest path) of your graph.
var pregel = require("@arangodb/pregel");pregel.start("sssp", "graphname", {source:"vertices/1337"})
There are two algorithms to find connected components in a graph. To find weakly connected components (WCC)you can use the algorithm named “connectedcomponents”, to find strongly connected components (SCC) you can use the algorithmnamed “scc”. Both algorithm will assign a component ID to each vertex.
A weakly connected components means that there exist a path from every vertex pair in that component.WCC is a very simple and fast algorithm, which will only work correctly on undirected graphs.Your results on directed graphs may vary, depending on how connected your components are.
In the case of SCC a component means every vertex is reachable from any other vertex in the same component.The algorithm is more complex than the WCC algorithm and requires more RAM, because each vertex needs to store much more state. Consider using WCC if you think your data may be suitable for it.
Hyperlink-Induced Topic Search (HITS)
HITS is a link analysis algorithm that rates Web pages, developed by Jon Kleinberg (The algorithm is also known as hubs and authorities).
The idea behind Hubs and Authorities comes from the typical structure of the web: Certain websites known as hubs, serve as large directories that are not actually authoritative on the information that they hold. These hubs are used as compilations of a broad catalog of information that leads users direct to other authoritative webpages.The algorithm assigns each vertex two scores: The authority-score and the hub-score. The authority score rates how many good hubs point to a particularvertex (or webpage), the hub score rates how good (authoritative) the vertices pointed to are. For more see
Our version of the algorithmconverges after a certain amount of time. The parameter threshold can be used to set a limit for the convergence (measured as maximum absolute difference of the hub and authority scores between the current and last iteration)When you specify the result field name, the hub score will be stored in <result field>_hub and the authority score in <result field>_auth.The algorithm can be executed like this:
var pregel = require("@arangodb/pregel");var handle = pregel.start("hits", "yourgraph", {threshold:0.00001, resultField: "score"});
Vertex Centrality
Effective Closeness
A common definitions of centrality is the closeness centrality (or closeness). The closeness of a vertex in a graph is the inverse average length of the shortest path between the vertex and all other vertices. For vertices x, y and shortest distance d(y,x) it is defined as
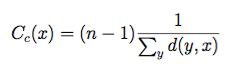
Effective Closeness approximates the closeness measure. The algorithm works by iteratively estimating the numberof shortest paths passing through each vertex. The score will approximates the real closeness score, sinceit is not possible to actually count all shortest paths due to the horrendous O(n^2 * d) memory requirements. The algorithm is from the paper Centralities in Large Networks: Algorithms and Observations (U Kang et.al. 2011)
ArangoDBs implementation approximates the number of shortest path in each iteration by using a HyperLogLog counter with 64 buckets. This should work well on large graphs and on smaller ones as well. The memory requirements should be O(n * d) where n is the number of vertices and d the diameter of your graph. Each vertex will store a counter for each iteration of thealgorithm. The algorithm can be used like this
const pregel = require("@arangodb/pregel");const handle = pregel.start("effectivecloseness", "yourgraph", {resultField: "closeness"});
LineRank
Another common measure is the betweenness* centrality: It measures the number of times a vertex is part of shortest paths between any pairs of vertices. For a vertex v betweenness is defined as
Where the σ represents the number of shortest paths between x and y, and σ(v) represents the number of paths also passing through a vertex v. By intuition a vertex with higher betweenness centrality will have more informationpassing through it.
LineRank approximates the random walk betweenness of every vertex in a graph. This is the probability that someone starting onan arbitrary vertex, will visit this node when he randomly chooses edges to visit.The algorithm essentially builds a line graph out of your graph (switches the vertices and edges), and then computes a score similar to PageRank.This can be considered a scalable equivalent to vertex betweenness, which can be executed distributedly in ArangoDB. The algorithm is from the paper Centralities in Large Networks: Algorithms and Observations (U Kang et.al. 2011)
const pregel = require("@arangodb/pregel");const handle = pregel.start("linerank", "yourgraph", {"resultField": "rank"});
Graphs based on real world networks often have a community structure. This means it is possible to find groups of vertices such that each vertex group is internally more densely connected than outside the group.This has many applications when you want to analyze your networks, for exampleSocial networks include community groups (the origin of the term, in fact) based on common location, interests, occupation, etc.
Label Propagation
Label Propagation can be used to implement community detection on large graphs. The idea is that eachvertex should be in the community that most of his neighbors are in. We iteratively determine this by firstassigning random Community ID’s. Then each iteration, a vertex will send it’s current community ID to all his neighbor vertices. Then each vertex adopts the community ID he received most frequently during the iteration.
The algorithm runs until it converges,which likely never really happens on large graphs. Therefore you need to specify a maximum iteration bound which suits you.The default bound is 500 iterations, which is likely too large for your application.Should work best on undirected graphs, results on directed graphs might vary depending on the density of your graph.
const pregel = require("@arangodb/pregel");const handle = pregel.start("labelpropagation", "yourgraph", {maxGSS:100, resultField: "community"});
Speaker-Listener Label Propagation
The (SLPA) can be used to implement community detection.It works similar to the label propagation algorithm,but now every node additionally accumulates a memory of observed labels (instead of forgetting all but one label).
Before the algorithm run, every vertex is initialized with an unique ID (the initial community label).During the run three steps are executed for each vertex:
- Current vertex is the listener all other vertices are speakers
- Each speaker sends out a label from memory, we send out a random label with a probabilityproportional to the number of times the vertex observed the label
- The listener remembers one of the labels, we always choose the most frequently observed label
const handle = pregel.start("slpa", "yourgraph", {maxGSS:100, resultField: "community"});
You can also execute SLPA with the maxCommunities parameter to limit the number of output communities.Internally the algorithm will still keep the memory of all labels, but the output is reduced to just he n most frequentlyobserved labels.
Limits
Pregel algorithms in ArangoDB will by default store temporary vertex and edge data in main memory. For largedatasets this is going to cause problems, as servers may run out of memory while loading the data.
To avoid servers from running out of memory while loading the dataset, a Pregel job can be started with theattribute useMemoryMaps set to true. This will make the algorithm use memory-mapped files as a backingstorage in case of huge datasets. Falling back to memory-mapped files might make the computation disk-bound, butmay be the only way to complete the computation at all.
In general it is also recommended to set the store attribute of Pregel jobs to true to make a job storeits value on disk and not just in main memory. This way the results are removed from main memory once a Pregel job completes. If the store attribute is explicitly set to false, result sets of completed Pregel runswill not be removed from main memory until the result set is explicitly discarded by a call to the cancelfunction (or a shutdown of the server).


