1. 目前已有一些方法，如DeepWalk,LINE,PTE,node2vec ，它们在实践中得到了有效的证明，但是背后的理论机制尚不了解。

   事实上在 Word Embedding 任务中，带负采样的 SkipGram 模型已经被证明等价于一个 word-context 矩阵的隐式分解，但是还不清楚word-context 矩阵和网络结构之间的关系。另外，尽管 DeepWalk,LINE,PTE,node2vec 之间看起来很相似，但是缺乏对其底层连接更深入的理解。

   论文《Network Embedding as Matrix Factorization: Unifying DeepWalk, LINE, PTE, and node2vec》 证明了 DeepWalk,LINE,PTE,node2vec 在理论上等价于隐式矩阵分解，并给出了每个模型的矩阵形式的闭式解。另外论文还发现：

   • 当上下文窗口大小 时，LINE 可以被视为是 DeepWalk 的特例。
   • PTE 作为 LINE 的扩展，实际上它是多个网络联合矩阵的隐式分解。
   • DeepWalk 的隐式矩阵分解和图拉普拉斯算子之间存在理论联系，基于这种联系作者提出了一个新的算法 NetMF 来近似 DeepWalk 隐式矩阵分解的闭式解。

   最后作者使用 SVD 对每个算法的矩阵进行显式分解，通过实验证明了 NetMF 优于其它的几个模型。

15.1.1 LINE

1. 给定一个带权无向图 ，LINE(2nd) 任务是学到两个representation 矩阵 ：

   • vertex represetation 矩阵 ：第 行 为顶点 作为vertex 时的 embedding 向量。
   • context representation 矩阵 ：第 行 为顶点 作为contex 时的 embedding 向量。

   LINE(2nd) 的目标函数为：

   其中：

   • 为 sigmoid 函数

   • 为负采样系数

   • 为用于产生负样本的 noise 分布，在 LINE 原始论文中使用经验分布： ，其中 为顶点 j 的加权 degree ：

2. 本文我们选择 ，因为这种形式的经验分布将得到一个闭式解。定义 为所有顶点的加权 degree 之和，则有：

   

   我们重写目标函数为：

   我们在图 的所有顶点上计算，从而得到期望为：

   因此有：

   

   则对于每一对顶点 (i,j)，其局部目标函数local objective function 为：

   定义 ，根据 《NeuralWord Embedding as Implicit Matrix Factorization》 的结论：对于一个足够大的 embedding 维度， 每个 之间可以认为是相对独立的。因此我们有：

   

   为求解目标函数极大值，我们令偏导数为零，则有：

   这个方程有两个闭式解：

   • ：其解为虚数，不予考虑。
   • ：有效解。

   因此有：

   

   定义对角矩阵 ，则 LINE(2nd) 对应于矩阵分解：

   

   .

15.1.2 PTE

1. PTE 将文本网络分为三个子网络，假设单词集合为 ，文档集合为 ，标签集合为 ：

   • word-word 子网 ：每个 word 是一个顶点，边的权重为两个 word 在大小为 T 的窗口内共现的次数。

     假设其邻接矩阵为 ，定义 为 第 行的元素之和， 定义 为 第 列的元素之和。由于 为无向图，因此 为对称矩阵，所以有 。

     定义对角矩阵 ， ，它们分别由 的各行之和、各列之和组成。

   • word-document 子网 ：每个 word 和 document 都是一个顶点，边的权重是word 出现在文档中的次数。它是一个二部图，因此 不是对称矩阵，因此 。

     同样的我们定义对角矩阵 ， ，它们分别由 的各行之和、各列之和组成。

   • word-label 子网 ：每个 word 和 label 都是一个顶点，边的权重为 word 出现在属于这个 label 的文档的篇数。它也是一个二部图，因此 不是对称矩阵，因此 。

     同样的我们定义对角矩阵 ， ，它们分别由 的各行之和、各列之和组成。

   PTE 的损失函数为：

   

   其中 分别为三个子网中的量， 为三个超参数来平衡不同子网的损失， 为负采样系数。

   根据前面的结论有：

   

   令：

   则有 ，且有：

2. 根据 PTE 论文， 需要满足：

   这是因为PTE 在训练期间执行边采样，其中边是从三个子网中交替采样得到。

15.1.3 DeepWalk

1. DeepWalk 首先通过在图上执行随机游走来产生一个 corpus ，然后在 上训练 SkipGram 模型。这里我们重点讨论带负采样的 SkipGram 模型skipgram with negative sampling:SGNS 。整体算法如下所示：

   • 输入：

     • 图
     • 窗口大小
     • 随机游走序列长度
     • 总的随机游走序列数量

   • 输出：顶点的 embedding 矩阵

   • 算法步骤：

     • 迭代： ，迭代过程为：

       • 根据先验概率分布 随机选择一个初始顶点 。

       • 在图 上从初始顶点 开始随机游走，采样得到一条长度为 的顶点序列 。

       • 统计顶点共现关系。对于窗口位置 ：

         • 考虑窗口内第 个顶点 ：

           • 添加 vertex-context 顶点对 到 中。
           • 添加 vertex-context 顶点对 到 中。
     • 然后在 上执行负采样系数为 的 SGNS 。

2. 根据论文 《NeuralWord Embedding as Implicit Matrix Factorization》 ， SGNS 等价于隐式的矩阵分解：

   其中： 为语料库大小； 为语料库 中 共现的次数； 为语料库中 vertex 出现的总次数； 为语料库中 context 出现的总次数； 为负采样系数。

3. 定理一：定义，则当 时有：

   

   其中： 表述依概率收敛。

   其物理意义为：

   • 在所有正向转移过程中，vertex-context 在语料库中出现的概率等于： 出现的概率，乘以从 正向转移 步骤到达 的概率。
   • 在所有正向转移过程中，vertex-context 在语料库中出现的概率等于： 出现的概率，乘以从 正向转移 步骤到达 的概率。

   证明：

   首先介绍 S.N. Bernstein 大数定律：设 为一个随机变量的序列，其中每个随机变量具有有限的期望 和有限的方差 ，并且协方差满足：当 时， 。则大数定律 law of large numbers:LLN 成立。

   我们观察到：

   • ， 。因此有：

   • 基于我们对图的假设和随机游走的假设，则有： 发生的概率等于 的概率乘以 经过 步转移到 的概率。即：

   • 基于我们对图的假设和随机游走的假设，则有：当 时有：

     其中：第一项为 采样到 的概率；第二项为从 经过 步转移到 的概率；第三项为从 经过 步转移到 得概率；第四项为从 经过 步转移到 的概率。

   则有：

   当 时，从 经过 步转移到 的概率收敛到它的平稳分布，即 。即：

   因此有 。因此随机游走序列收敛到它的平稳分布。

   应用大数定律，则有：

   类似地，我们有：

   

   当 时，我们定义 为事件 的指示器，同样可以证明相同的结论。

4. 事实上如果随机游走序列的初始顶点分布使用其它分布（如均匀分布），则可以证明：当 时，有：

   因此定理一仍然成立。

5. 定理二：当 时，有：

   证明：

   注意到 ，应用定理一有：

   进一步的，考察 的边际分布和 的边际分布，当 时，我们有：

6. 定理三：在 DeepWalk 中，当 时有：

   因此DeepWalk 等价于因子分解：

   

   证明：

   利用定理二和continous mapping theorem，有：

   写成矩阵的形式为：

   

7. 事实上我们发现，当 时，DeepWalk 就成为了 LINE(2nd)， 因此 LINE(2nd) 是 DeepWalk 的一个特例。

15.1.4 node2vec

1. node2vec 是最近提出的 graph embedding 方法，其算法如下：

   • 输入：

     • 图
     • 窗口大小
     • 随机游走序列长度
     • 总的随机游走序列数量

   • 输出：顶点

   • 算法步骤：

     • 构建转移概率张量

     • 迭代： ，迭代过程为：

       • 根据先验概率分布 随机选择初始的两个顶点 。

       • 在图 上从初始顶点 开始二阶随机游走，采样得到一条长度为 的顶点序列 。

       • 统计顶点共现关系。对于窗口位置 ：

         • 考虑窗口内第 个顶点 ：

           • 添加三元组 到 中。
           • 添加三元组 到 中。
     • 然后在 上执行负采样系数为 的 SGNS 。

     注意：这里为了方便分析，我们使用三元组 ，而不是vertex-context 二元组。

2. node2vec 的转移概率张量 采取如下的方式定义：

   • 首先定义未归一化的概率：

     其中 表示在 的条件下， 的概率。

   • 然后得到归一化的概率：

3. 类似 DeepWalk ，我们定义：

   

   这里 为previous 顶点。

   定义 为 出现在 中出现的次数；定义 为 出现在 中出现的次数。

   定义二阶随机游走序列的平稳分布为 ，它满足： 。根据 Perron-Frobenius 定理，这个平稳分布一定存在。为了便于讨论，我们定义每个随机游走序列的初始两个顶点服从平稳分布 。

   定义高阶转移概率矩阵 。

   由于篇幅有限，这里给出 node2vec 的主要结论，其证明过程类似 DeepWalk ：

   

   因此 node2vec 有：

   尽管实现了 node2vec 的封闭形式，我们将其矩阵形式的公式留待以后研究。

4. 注意：存储和计算转移概率张量 以及对应的平稳分布代价非常高，使得我们难以对完整的二阶随机游走动力学过程建模。但是最近的一些研究试图通过对 进行低秩分解来降低时间复杂度和空间复杂度：

   

   由于篇幅限制，我们这里主要集中在一阶随机游走框架DeepWalk 上。

15.1.5 NetMF

1. 根据前面的分析我们将 LINE,PTE,DeepWalk,node2vec 都统一到矩阵分解框架中。这里我们主要研究 DeepWalk 矩阵分解，因为它比 LINE 更通用、比 node2vec 计算效率更高。

2. 首先论文引用了四个额外的定理：

   • 定理四：定义归一化的图拉普拉斯矩阵为 ，则它的特征值都是实数。

     而且，假设它的特征值从大到小排列 ，则有：

     

     进一步的，假设该图是连通图 （connected），并且顶点数量 ，则有： 。

     证明参考：Fan RK Chung. 1997. Spectral graph theory. Number 92. American Mathematical Soc.

   • 定理五：实对称矩阵的奇异值就是该矩阵特征值的绝对值。

     证明参考：Lloyd N Trefethen and David Bau III. 1997. Numerical linear algebra. Vol. 50. Siam.

   • 定理六：假设 为两个对称矩阵，假设将 的奇异值按照降序排列，则对于任意 ，以下不等式成立：

     

     证明参考：Roger A. Horn and Charles R. Johnson. 1991. Topics in Matrix Analysis. Cambridge University Press. https://doi.org/10.1017/CBO9780511840371

3. 考察 DeepWalk 的矩阵分解：

   忽略常量以及 element-wise 的 log 函数，我们关注于矩阵： 。

   根据定理四，实对称矩阵 存在特征值分解 ，其中 为正交矩阵、 为特征值从大到小构成的对角矩阵。

   根据定理三可知， ，并且 。

   考虑到 ，因此有：

   

   • 我们首先分析 的谱。显然，它具有特征值：

     

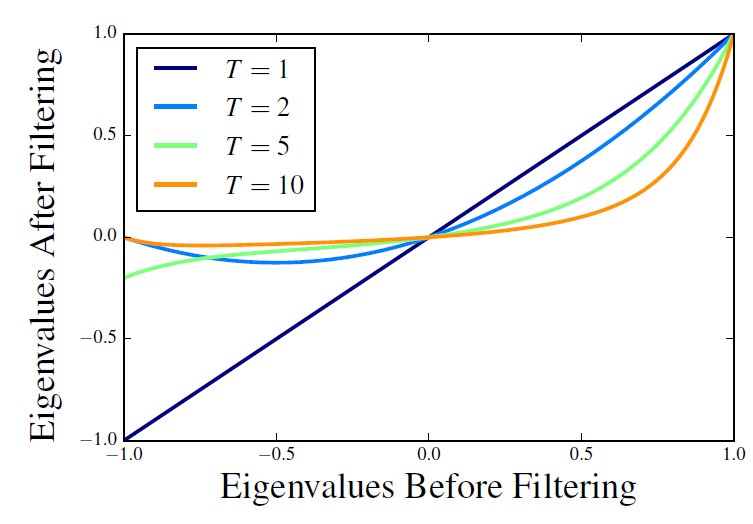
     这可以视为对 的特征值 进行一个映射 。这个映射可以视为一个滤波器，滤波器的效果如下图所示。可以看到：

     • 滤波器倾向于保留正的、大的特征值。
     • 随着窗口大小 的增加，这种偏好变得更加明显。

     即：随着 的增加，滤波器尝试通过保留较大的、正的特征值来近似低阶半正定矩阵。

     

   • 然后我们分析 的谱。

     根据定理五，矩阵 的奇异值可以根据其特征值的绝对值得到。我们将 进行降序排列，假设排列的顺序为 ，则有：

     考虑到每个 都是正数，因此我们可以将 的奇异值根据特征值 降序排列。假设排列的顺序为 ，则有：

     

     特别的， 为最小的 degree 。

     通过应用两次定理五，我们可以发现第 个奇异值满足：

     因此 的第 个奇异值的上界为 。

     另外，根据瑞利商，我们有：

     应用定理七，我们有：

     

4. 为了说明过滤器 的效果，我们分析了 Cora 数据集对应的引文网络。我们将引文链接视为无向边，并选择最大连通分量 largest connected component 。

   我们分别给出了 、 以及 按照降序排列的特征值，其中 。

   • 对于 ，最大的特征值为 ，最小特征值为 。

   • 对于 ，我们发现：它的所有负特征值以及一些小的正特征值都被过滤掉了 filtered out 。

   • 对于 ，我们发现：

     • 它的奇异值（即特征值的绝对值）被 的奇异值所限制 bounded 。
     • 它的最小特征值的被 的特征值所限制 bounded 。

5. 基于前面的理论分析，我们提出了一个矩阵分解框架 NetMF ，它是对 DeepWalk 和 LINE 的改进。

   为表述方便，我们定义：

   

   因此 对应于 DeepWalk 的矩阵分解。

   • 对于很小的 ，我们直接计算 并对 进行矩阵分解。

     考虑到直接对 进行矩阵分分解难度很大，有两个原因：

     • 当 时， 的行为未定义。
     • 是一个巨大的稠密矩阵，计算复杂度太高。

     受到 Shifted PPMI 启发，我们定义 。这使得 中每个元素都是有效的，并且 是稀疏矩阵。然后我们对 进行奇异值分解，并使用它的 top 奇异值和奇异向量来构造embedding 向量。

   • 对于很大的 ，直接计算 的代价太高。我们提出一个近似算法，主要思路是：根据 和归一化拉普拉斯算子之间的关系来近似 。

     • 首先我们对 进行特征值分解，通过它的 top 个特征值和特征向量来逼近 。

       由于只有 top 个特征值被使用，并且涉及的矩阵是稀疏的，因此我们可以使用 Arnoldi 方法来大大减少时间。

     • 然后我们通过 来逼近 。

6. 算法：

   • 输入：

     • 图
     • 窗口大小

   • 输出：顶点的 embedding 矩阵

   • 算法步骤：

     • 如果 较小，则计算：

       如果 较大，则执行特征值分解： 。然后计算：

       

     • 执行 维的 SVD 分解： 或者 。

     • 返回 作为网络 embedding。

7. 对于较大的 ，可以证明 逼近 的误差上界，也可以证明 逼近 的误差上界。

   定理八：令 为矩阵的 Frobenius 范数，则有：

   证明：

   • 第一个不等式：可以通过 F 范数的定义和前面的定理七来证明。

   • 第二个不等式：不失一般性我们假设 ，则有：

     第一步成立是因为： 对于 有 ；第二步成立是因为： 。因此有 。

     另外，根据 和 的定义有：

     

     因此有： 。

8. DeepWalk 尝试通过随机游走来对顶点抽样，从而期待用经验分布来逼近真实的 vertex-context 分布。尽管大数定律可以保证这种方式的收敛性，但是实际上由于真实世界网络规模较大，而且实际随机游走的规模有限（随机游走序列的长度、序列的数量），因此经验分布和真实分布之间存在gap 。这种 gap 会对 DeepWalk 的性能产生不利影响。

   NetMF 通过直接建模真实的 vertex-context 分布，从而降低了这种 gap ，从而得到比 DeepWalk 更好的效果。

15.2 实验

1. 作者在多标签顶点分类任务中评估 NetMF 的性能。

2. 数据集：

   • BlogCatalog 数据集：由博客作者提供的社交关系网络。标签代表作者提供的主题类别。
   • Flickr 数据集：Flickr网站用户之间的关系网络。标签代表用户的兴趣组，如“黑白照片”。
   • Protein-Protein Interactions:PPI：该数据集包含蛋白质和蛋白质之间的关联，标签代表基因组。
   • Wikipedia 数据集：来自维基百科，包含了英文维基百科 dump 文件的前 个字节中的单词共现网络。顶点的标签表示通过Stanford POS-Tagger推断出来的单词词性Part-of-Speech:POS 。

3. Baseline 模型：我们将 NetMF(T=1)、NetMF(T=10) 和 LINE,DeepWalk 进行比较。

   • 所有模型的 embedding 维度都是 128 维。
   • 对于 NetMF(T=10) ，我们在 Flickr 数据集上选择 ，在其它数据集上选择 。
   • 对于 DeepWalk ，我们选择窗口大小为 10、随机游走序列长度 40、每个顶点开始的随机游走序列数量为 80 。

   我们重点将 NetMF(T=1) 和 DeepWalk 进行比较，因为二者窗口大小都为 1 ；重点将 NetMF(T=10) 和 DeepWalk 进行比较，因为二者窗口大小都为 10 。

4. 和 DeepWalk 相同的实验步骤，我们首先训练整个网络的 embedding，然后随机采样一部分标记样本来训练一个one-vs-rest 逻辑回归分类模型，剩余的顶点作为测试集。我们评估测试集的 Micro-F1 指标和 Macro-F1 指标。为了确保实验结果可靠，每个配置我们都重复实验 10 次，并报告测试集指标的均值。

   对于 BlogCatalog,PPI,Wikipedia 数据集，我们考察分类训练集占比 10%~90% 的情况下，各模型的性能；对于 Flickr 数据集，我们考察分类训练集占比 1%~10% 的情况下，各模型的性能。

   完成的实验结果如下图所示。可以看到：NetMF(T=1) 相对于 LINE(2nd) 取得了性能的提升，NetMF(T=10) 相对于 DeepWalk 也取得了性能提升。

   • 在 Wikipedia 数据集中，窗口更小的 NetMF(T=1) 和 LINE(2nd) 效果更好。这表明：短期依赖足以建模 Wikipedia 网络结构。

   如下表所示，大多数情况下当标记数据稀疏时，NetMF 方法远远优于 DeepWalk 和 。