可以考虑用一个 阶矩阵 来近似代替 。

先看海森矩阵满足的条件： 。

• 令 。则有：，或者 。

  这称为拟牛顿条件。

• 根据牛顿法的迭代： ，将 在 的一阶泰勒展开：

  当 是正定矩阵时，总有 ，因此每次都是沿着函数递减的方向迭代。

如果选择 作为 的近似时， 同样要满足两个条件：

• 必须是正定的。

• 满足拟牛顿条件： 。

  因为 是给定的初始化条件，所以下标从 开始。

按照拟牛顿条件，在每次迭代中可以选择更新矩阵 。

正定矩阵定义：设 是 阶方阵，如果对任何非零向量 ，都有 ，就称 正定矩阵。

• 正定矩阵判定：

  • 判定定理1：对称阵 为正定的充分必要条件是： 的特征值全为正。
  • 判定定理2：对称阵 为正定的充分必要条件是： 的各阶顺序主子式都为正。
  • 判定定理3：任意阵 为正定的充分必要条件是： 合同于单位阵。

• 正定矩阵的性质：

  • 正定矩阵一定是非奇异的。奇异矩阵的定义：若 阶矩阵 为奇异阵，则其的行列式为零，即 。
  • 正定矩阵的任一主子矩阵也是正定矩阵。
  • 若 为 阶对称正定矩阵，则存在唯一的主对角线元素都是正数的下三角阵 ，使得 ，此分解式称为 正定矩阵的乔列斯基（）分解。
  • 若 为 阶正定矩阵，则 为 阶可逆矩阵。

• 所有特征值大于零的对称矩阵也是正定矩阵。

合同矩阵：两个实对称矩阵 和 是合同的，当且仅当存在一个可逆矩阵 ，使得

• 的合同变换：对某个可逆矩阵 ，对 执行 。

DFP算法( Davidon-Fletcher-Powell) 选择 的方法是：

假设每一步迭代中 是由 加上两个附加项构成：，其中 是待定矩阵。此时有：。

为了满足拟牛顿条件，可以取：。

这样的 不止一个。例如取 ：

可以证明：如果初始矩阵 是正定的，则迭代过程中每个矩阵 都是正定的。

DFP算法：

• 输入：

  • 目标函数
  • 梯度
  • 精度要求

• 输出： 的极小值点

• 算法步骤：

  • 选取初始值 , 取 为正定对称矩阵，置 。

  • 迭代，停止条件为：梯度收敛。迭代步骤为：

    • 计算 。

    • 若 ， 则停止计算，得到近似解 。

    • 若 ， 则：

      • 计算 。
      • 一维搜索：求 ： 。
      • 设置 。
      • 计算 。若 ， 则停止计算，得到近似解 。
      • 否则计算 ，置 ，继续迭代。

是最流行的拟牛顿算法。 DFP算法中，用 逼近 。换个角度看，可以用矩阵 逼近海森矩阵 。此时对应的拟牛顿条件为： 。

令： ，有： 。

可以取 。寻找合适的 ，可以得到 BFGS 算法矩阵的 的迭代公式：

可以证明，若 是正定的，则迭代过程中每个矩阵 都是正定的。

BFGS算法：

• 输入：

  • 目标函数
  • 梯度
  • 精度要求

• 输出： 的极小值点

• 算法步骤：

  • 迭代，停止条件为：梯度收敛。迭代步骤为：

    • 计算 。

    • 若 ， 则停止计算，得到近似解 。

    • 若 ， 则:

      • 由 求出 。

        这里表面上看需要对矩阵求逆。但是实际上 有迭代公式。根据Sherman-Morrison 公式以及 的迭代公式，可以得到 的迭代公式。

      • 一维搜索：求 ： 。

      • 设置 。

      • 计算 。若 ， 则停止计算，得到近似解 。

      • 否则计算 ，置 ，继续迭代。

算法中，每一次 增加的方向是 的方向。增加的幅度由 决定，若跨度过大容易引发震荡。

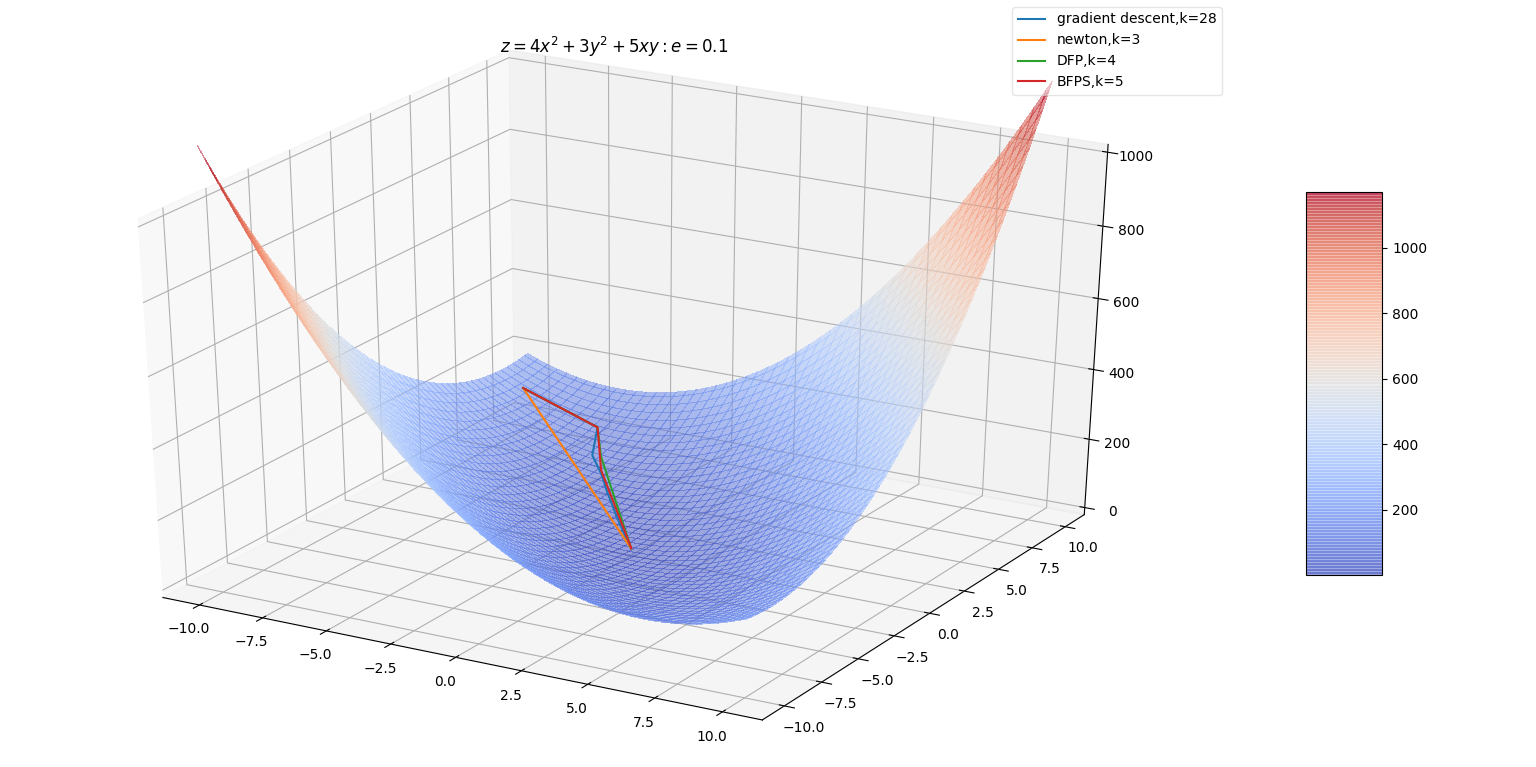
若记 ，则对式子：

使用两次Sherman-Morrison公式可得：

公式：假设 是 阶可逆矩阵， 是 维列向量，且 也是可逆矩阵，则：

.